Geschichte der klassischen Astronomie im Überblick kurz dargestellt



Zur Einführung zwei bekannte Bilder, die oft falsch eingeschätzt werden:



Dass dieses Bild nicht der Realität entspricht, bzw. die Erde keine Scheibe, sondern eine Kugel ist, war schon den Babyloniern und den Griechen bekannt. Auch zum mittelalterlichen wissenschaftlichen Weltbild gehörte natürlich die Kugelgestalt der Erde. Wer heute das Mittelalter mit der Erde als Scheibe in Verbindung bringt, offenbart Bildungslücken. Dieses Bild des Randes der Erdscheibe ist wohl eher als amüsante Satire gedacht.

Dieser berühmte Holzstich aus dem 19. Jahrhundert ist kaum als Propaganda für eine Scheiben-Form der Erde gedacht. Das Bild soll zeigen, dass der denkende Mensch mit seinem Geist in 'Welten' Einblick nehmen kann, die seinen Sinnen bzw. seinen unmittelbaren Alltagserfahrungen verborgen sind.







Vorgeschichte: Einer der Ursprünge wissenschaftlicher Astronomie

Die erstaunlichen Kenntnisse der Babylonier umfassten bereits folgendes:


Rekonstruktion des Stufenturms von Babylon mit Umgebung
(Ministry of Information, Bagdad)
  • Das Fixsternbild ist konstant und dreht täglich von Ost nach West über dem Beobachtungsort [Heutige Erklärung: Erdrotation]. Jahreszeitlich 'pendelt' es deutlich erkennbar zwischen Norden und Süden [Heutige Erklärung: Sonnenumkreisung der Erde zusammen mit schräger Erdachse].

  • In diesem Fixsternbild verändern mitunter einige helle Punkte ihre Position und halten sich nicht an die Fixsternkonstanz --> Planeten ('Wandelsterne').

  • Diese Planeten führen gegenüber dem Fixsternenbild mitunter Schleifenbewegungen aus (im Verlauf von Wochen), sind also kurzzeitig rückläufig --> Planetenschleifen (siehe später).





Aristoteles (384-322 v. Chr.)



Er plausibilisierte die Kugelgestalt der Erde durch folgende Überlegung:


Bei gewöhnlichen Mondphasen (Neumond, Viertelmond, Halbmond, Dreiviertelmond, Vollmond) krümmt sich die Eigen-Schatten-Grenze des Mondes immer von der Mondmitte weg, was im folgenden Bild die obere Reihe zeigt.

Aristoteles beobachtete, dass demgegenüber bei einer Mondfinsternis der Schatten (jetzt nicht des Mondes Eigenschatten, sondern der Schatten der Erde) beim 'Wandern' über den gesamten Mond immer auf die gleiche Seite gebogen ist, was im folgenden Bild die untere Reihe zeigt:




Dies dürfte das beste Argument für die von Denkern damals schon länger vermutete Kugelgestalt der Erde sein (neben den Beobachtungen von Krümmungserscheinungen am Meer beim 'Auf- oder Untertauchen' von Schiffen in der Ferne).


Im Folgenden eine Amateur-Aufnahme der Mondfinsternis vom 27/28.07.2018. Der Erdschatten schiebt sich über den Mond bis zur vollen Verfinsterung des Mondes. Das rötliche 'Restleuchten' des Mondes bei der totalen Finsternis stammt von in der Erdatmosphäre gebrochenem roten Sonnenlichtanteil:





Eratosthenes (276-195 v. Chr.)



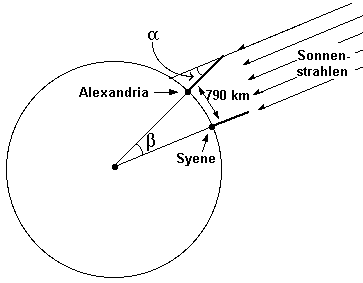Er berechnete als Erster den Umfang der Erde:

Während in Syene (Assuan) die Sonne senkrecht stand (und den Grund eines Brunnens erhellte), bildete sie gleichzeitig im ca 790 km nördlich gelegenen Alexandria bei einem Obelisken einen Schatten unter einem Winkel von 7.2° (Alpha) (siehe Bild). Somit war der (Wechsel-)Winkel zwischen Assuan und Alexandria beim Erdmittelpunkt auch 7.2° (Beta). Ein einfacher Dreisatz ergab jetzt den Erdumfang:

                   7.2° --->     790 km
                 360.0° --->  39'500 km


Das Resultat stimmt erstaunlich gut! Die Zahlen variieren je nach Quelle etwas, da der Wert der damaligen ägyptischen Stadie nicht genau bekannt ist.




Situation in Alexandria:

 Situation in Syene (Assuan):

 Situation auf der Erdkugel:






Aristarchos von Samos (310-230 v. Chr.)



Er untersuchte geometrisch die Grössenverhältnisse von Erde, Mond und Sonne, sowie das Abstandsverhältnis (Erde - Mond) zu (Erde - Sonne):






Von der Erde aus betrachtet, erscheinen Sonne und Mond bekanntlich gleich gross. Auf Grund des abgebildeten Dreiecks (Winkel Alpha 90°) bei Halbmond (Bild nicht massstäblich) erkannte nun Aristarch zusätzlich, dass die Sonne dann wesentlich weiter von der Erde entfernt sein muss, als der Mond.


Seine Überlegung:

Bei Halbmond (siehe Bild) muss der Dreieckswinkel beim Mond ein rechter sein. Für den schwer messbaren Winkel Alpha [der notwendige genaue Zeitpunkt [wann exakt ist Halbmond] für die Messung ist schwierig anzugeben] fand Aristarch 87°. Daraus ergab sich auf einem "Zeichnungsblatt" ein Entfernungsverhältnis von ca 1 : 19. (In Wirklichkeit ist Alpha 89°51' und damit das Verhältnis 1 : 400. Trotz dieses Fehlers ist der Grundgedanke richtig und liess den folgenden richtigen Schluss zu:

Da Mond und Sonne am Himmel gleich gross erscheinen, muss die Sonne (nach Aristarch) den 19-fachen Durchmesser des Mondes (also das 19^3 = 6860-fache Volumen!) haben, da sie ja 19-mal weiter von der Erde entfernt ist, als der Mond. Doch wie gross ist der Mond? Aristarch verglich ihn mit der Grösse des Schattens, den die Erde bei einer Mondfinsternis auf den Mond wirft. (Weil die Sonne so weit entfernt ist, muss dieser Schatten ungefähr gleich gross sein, wie die Erde selbst). Aristarch schätzte den Schattendurchmesser ca 4-mal grösser als den des Mondes und schloss daraus, dass die Erde etwa den 4-fachen Durchmesser des Mondes haben müsse (was auch etwa stimmt) und daher wesentlich kleiner als die Sonne sein müsse. Und ebenso müsse demnach auch die Erde sehr viel kleiner als die Sonne sein.

Dieses Ergebnis machte Aristarch nachdenklich: Sollte die grosse Sonne wirklich die kleine Erde umkreisen? Aristarch konnte es nicht glauben und zog den Schluss, dass nicht die Erde, sondern die Sonne still stehe und von der kleinern Erde (mit ihrem Mond) umkreist werde! Damit war er seiner Zeit weit voraus.



Weiter



Eine Ebene nach oben