Eine Ebene zurück
|
"1° daneben ist doch nicht so schlimm ..." |
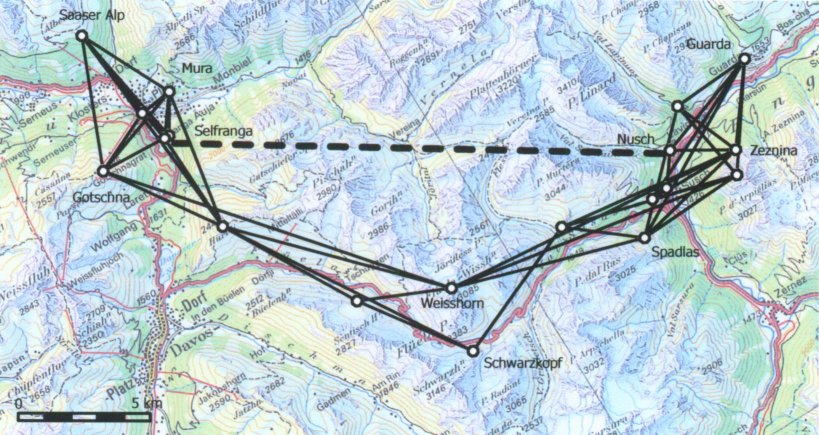
 Wenn ein Schütze im üblichen 300 m-Schiessstand um 1° daneben schiesst, folgt bei der Scheibe eine Abweichung von über 5 m, d. h. es wird irgendwo die über-über-nächste Scheibe getroffen. Um das "Schwarze" der eigenen Scheibe wenigstens noch am Rand zu treffen, ist eine Zielgenauigkeit von 0.057° (also ein gutes halbes Zehntelgrad) erforderlich.
Wenn ein Schütze im üblichen 300 m-Schiessstand um 1° daneben schiesst, folgt bei der Scheibe eine Abweichung von über 5 m, d. h. es wird irgendwo die über-über-nächste Scheibe getroffen. Um das "Schwarze" der eigenen Scheibe wenigstens noch am Rand zu treffen, ist eine Zielgenauigkeit von 0.057° (also ein gutes halbes Zehntelgrad) erforderlich.
 Bild:
Bild: